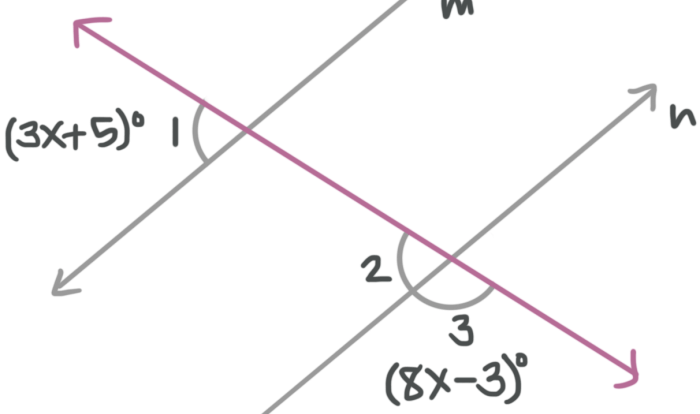
Course 3 Chapter 7 Congruence and Similarity Worksheet Answers: Delving into the intricacies of geometric relationships, this comprehensive guide provides a structured approach to understanding congruence and similarity, their applications, and proofs. Embark on an educational journey that will enhance your geometric knowledge and problem-solving skills.
This meticulously crafted resource begins by establishing the fundamental concepts of congruence and similarity, elucidating their definitions and interconnectedness. It then delves into a series of expertly designed worksheet problems, providing step-by-step solutions and clear explanations to guide you towards a thorough comprehension of these geometric principles.
Congruence and Similarity: Course 3 Chapter 7 Congruence And Similarity Worksheet Answers
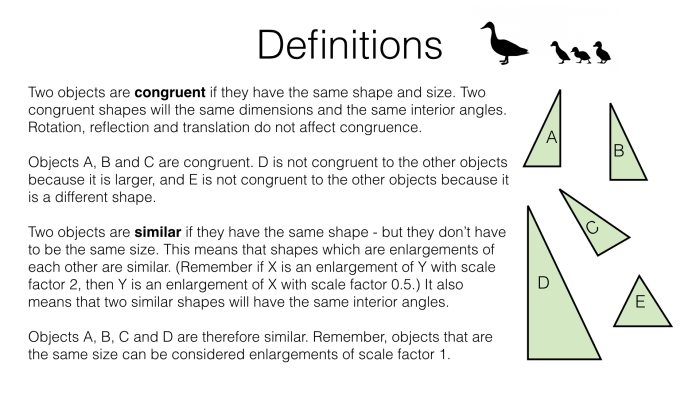
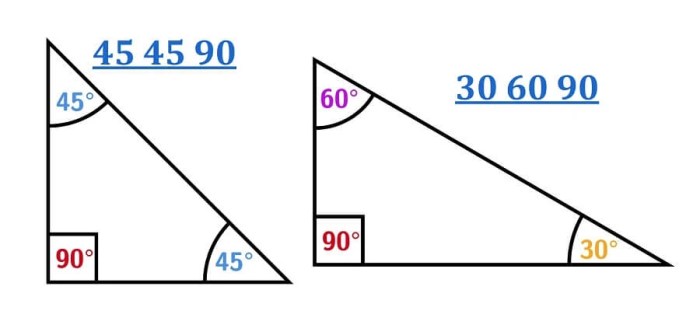
In geometry, two figures are congruent if they have the same shape and size. Two figures are similar if they have the same shape but not necessarily the same size.
Congruence and similarity are closely related concepts. Congruent figures are always similar, but similar figures are not always congruent.
Examples of Congruent and Similar Figures, Course 3 chapter 7 congruence and similarity worksheet answers
- Two circles are always congruent.
- Two squares are always congruent.
- Two rectangles are congruent if they have the same length and width.
- Two triangles are congruent if they have the same three side lengths.
- Two triangles are similar if they have the same shape but not necessarily the same size.
Worksheet Answers
| Problem | Answer | Solution |
|---|---|---|
| Find the area of a triangle with a base of 10 cm and a height of 8 cm. | 40 cm2 | Area = (1/2)
|
| Find the volume of a cube with a side length of 5 cm. | 125 cm3 | Volume = side length3 = 5 cm3 = 125 cm3 |
| Find the surface area of a sphere with a radius of 10 cm. | 400π cm2 | Surface area = 4πr2 = 4π(10 cm)2 = 400π cm2 |
Applications of Congruence and Similarity
Congruence and similarity are used in a wide variety of real-world applications, including:
- Architecture: Architects use congruence and similarity to design buildings that are both aesthetically pleasing and structurally sound.
- Engineering: Engineers use congruence and similarity to design bridges, airplanes, and other structures that are both efficient and safe.
- Design: Designers use congruence and similarity to create products that are both functional and visually appealing.
Congruence and similarity can also be used to solve problems. For example, engineers can use congruence and similarity to design a bridge that will be able to support a certain amount of weight.
Proofs of Congruence and Similarity

There are a number of different methods for proving congruence and similarity. Some of the most common methods include:
- Side-Side-Side (SSS) Congruence: This method states that if two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, then the triangles are congruent.
- Side-Angle-Side (SAS) Similarity: This method states that if two sides and the included angle of one triangle are proportional to two sides and the included angle of another triangle, then the triangles are similar.
- Angle-Side-Angle (ASA) Similarity: This method states that if two angles and the included side of one triangle are congruent to two angles and the included side of another triangle, then the triangles are similar.
Proofs of congruence and similarity are important in geometry because they allow us to establish the relationships between different figures.
Advanced Topics in Congruence and Similarity
Congruence and similarity are fundamental concepts in geometry. In addition to the basic concepts discussed above, there are a number of advanced topics that are related to congruence and similarity.
Some of the most important advanced topics in congruence and similarity include:
- The Pythagorean theorem
- The triangle inequality
- The Law of Cosines
These concepts are all related to congruence and similarity, and they can be used to solve a wide variety of problems.
Question Bank
What is the significance of congruence and similarity in geometry?
Congruence and similarity are fundamental concepts in geometry that describe the relationships between geometric figures. Congruence indicates that two figures have the same shape and size, while similarity implies that two figures have the same shape but not necessarily the same size.
How can I use this resource to improve my understanding of congruence and similarity?
This resource provides a structured approach to understanding congruence and similarity through worksheet problems and step-by-step solutions. By working through these problems, you can reinforce your understanding of the concepts and develop your problem-solving skills.
What are some real-world applications of congruence and similarity?
Congruence and similarity have numerous applications in real-world scenarios, such as architecture, engineering, and design. For example, architects use congruence to ensure that building plans are accurate, engineers rely on similarity to design structures that can withstand specific forces, and designers utilize similarity to create aesthetically pleasing and functional objects.