Special right triangles 30 60 90 worksheet – Embark on an illuminating journey into the realm of special right triangles, where the enigmatic 30-60-90 triangle unveils its captivating properties and practical applications. Delve into this comprehensive guide, meticulously crafted to unravel the secrets of these geometric wonders.
Within these pages, you will discover the defining characteristics of special right triangles, unraveling the mysteries of the 30-60-90 triangle. Explore its remarkable side ratios, angle measures, and the profound implications of the Pythagorean theorem. Equip yourself with a repertoire of formulas that empower you to effortlessly calculate side lengths and angles.
Special Right Triangles 30-60-90 Worksheet: Special Right Triangles 30 60 90 Worksheet
Introduction
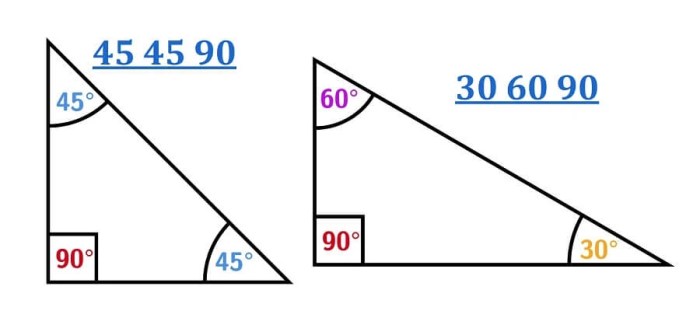
Special right triangles are triangles that have specific angle measures that make their side lengths predictable. The most common special right triangle is the 30-60-90 triangle. In this triangle, one angle measures 30 degrees, another angle measures 60 degrees, and the remaining angle measures 90 degrees.
This triangle is significant because its side lengths are related in a simple ratio, making it useful in many applications.
Properties of 30-60-90 Triangles, Special right triangles 30 60 90 worksheet
The side ratios of a 30-60-90 triangle are as follows:
- The hypotenuse is twice the length of the shorter leg.
- The longer leg is √3 times the length of the shorter leg.
The Pythagorean theorem can be used to find the length of any side of a 30-60-90 triangle if you know the lengths of the other two sides. The Pythagorean theorem states that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
In the case of a 30-60-90 triangle, this means that:
hypotenuse² = shorter leg² + longer leg²
Applications of 30-60-90 Triangles
30-60-90 triangles are used in a variety of real-world applications, including:
- Architecture: 30-60-90 triangles are used to design roofs, stairs, and other structures.
- Engineering: 30-60-90 triangles are used to calculate forces and moments in structures.
- Geometry: 30-60-90 triangles are used to solve geometry problems involving angles and side lengths.
Worksheet Activities
This worksheet includes a variety of problems involving 30-60-90 triangles. Use the properties discussed earlier to solve the problems.
- Find the length of the hypotenuse of a 30-60-90 triangle with a shorter leg of 5 cm.
- Find the length of the longer leg of a 30-60-90 triangle with a hypotenuse of 10 cm.
- A ladder is leaning against a wall. The bottom of the ladder is 4 feet from the wall, and the top of the ladder is 6 feet above the ground. What is the length of the ladder?
Helpful Answers
What is the significance of special right triangles?
Special right triangles, such as the 30-60-90 triangle, possess unique properties that make them invaluable in various applications. Their side ratios and angle measures simplify calculations and provide insights into geometric relationships.
How is the Pythagorean theorem applied to 30-60-90 triangles?
The Pythagorean theorem is a cornerstone for understanding 30-60-90 triangles. It establishes a relationship between the lengths of the sides, allowing for the calculation of unknown side lengths based on the known ones.
What are some real-world applications of 30-60-90 triangles?
30-60-90 triangles find practical applications in fields such as architecture, engineering, and surveying. They are used to determine heights, distances, and angles in various contexts, from designing buildings to navigating landscapes.