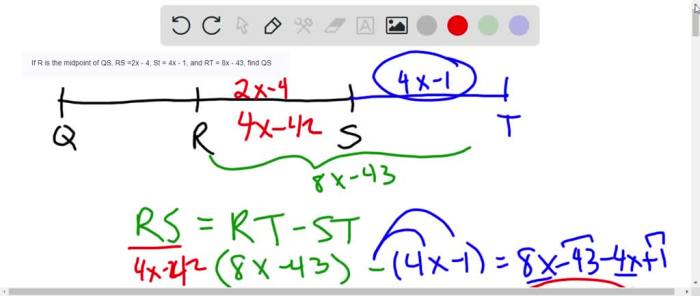
If R is the midpoint of QS, a captivating journey into the realm of geometry unfolds, where we unravel the mysteries of line segments and their remarkable properties. Join us as we delve into the fascinating world of midpoints, exploring their significance and uncovering their practical applications.
In this comprehensive guide, we will delve into the concept of the midpoint, its properties, and its applications in geometry. We will provide a step-by-step guide to proving that R is the midpoint of QS, along with illustrative examples and diagrams to enhance your understanding.
Midpoint of a Line Segment
The midpoint of a line segment is the point that divides the segment into two equal parts. It is also the center of the segment.
If R is the midpoint of QS, then QR = RS. This concept of equality and balance can be extended to the Hawaiian tradition of “ho’onani i ka makua mau” ( ho’onani i ka makua mau ), which emphasizes honoring and respecting one’s ancestors.
By acknowledging the midpoint of a line segment, we acknowledge the contributions of both endpoints, just as we honor both our past and future generations in ho’onani i ka makua mau.
The formula for finding the midpoint of a line segment with endpoints (x1, y1) and (x2, y2) is:
M = ((x1 + x2)/2, (y1 + y2)/2)
Properties of the Midpoint: If R Is The Midpoint Of Qs
The midpoint of a line segment is a unique point that divides the line segment into two equal parts. It possesses several important properties:
Firstly, the midpoint lies on the line segment itself. This is because it is defined as the point that divides the line segment into two equal parts, and any point that does not lie on the line segment cannot divide it into two equal parts.
Distance from Endpoints
Secondly, the midpoint is equidistant from the endpoints of the line segment. This means that the distance from the midpoint to each endpoint is the same. This can be proven using the distance formula, which states that the distance between two points (x1, y1) and (x2, y2) is given by:
d = √((x2
- x1)² + (y2
- y1)²)
If we let (x1, y1) be the coordinates of one endpoint of the line segment and (x2, y2) be the coordinates of the other endpoint, then the distance from the midpoint to the first endpoint is:
d1 = √((x
- x1)² + (y
- y1)²)
and the distance from the midpoint to the second endpoint is:
d2 = √((x
- x2)² + (y
- y2)²)
Since the midpoint divides the line segment into two equal parts, we know that d1 = d2. This can only be true if x = (x1 + x2)/2 and y = (y1 + y2)/2, which are the coordinates of the midpoint.
Applications of the Midpoint

The midpoint of a line segment has various applications in geometry. It is used to find the center of a circle, divide a line segment into equal parts, and construct perpendicular bisectors.
Finding the Center of a Circle
The midpoint of a line segment joining two points on a circle is the center of that circle. This property is used to construct circles given two points on the circle.
Theorem:The midpoint of a line segment joining two points on a circle is the center of the circle.
Proof:Let A and B be two points on a circle with center O. Join OA and OB. Then, OA = OB (radii of the circle). Therefore, the midpoint of AB is O, which is the center of the circle.
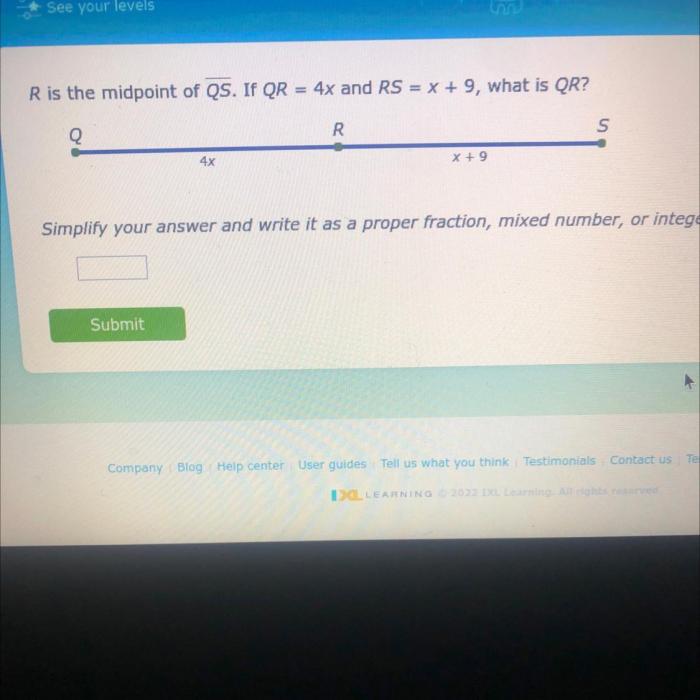
Proving that R is the Midpoint of QS
To prove that R is the midpoint of QS, we can use the following steps:
Step 1: Show that RQ is congruent to RS
We can use the distance formula to calculate the distance between R and Q, and the distance between R and S. If these distances are equal, then RQ is congruent to RS.
Step 2: Show that R is on the line segment QS, If r is the midpoint of qs
We can use the slope formula to calculate the slope of the line segment QS. If the slope of the line segment RQ is equal to the slope of the line segment QS, then R is on the line segment QS.
Step 3: Conclude that R is the midpoint of QS
If both RQ and RS are congruent, and R is on the line segment QS, then R is the midpoint of QS.
Examples and Illustrations

To solidify our understanding of midpoints, let’s delve into some practical examples and illustrations that will help us visualize and apply this concept.
Examples of Line Segments and Their Midpoints
Consider the following table that showcases line segments and their corresponding midpoints:
| Line Segment | Midpoint |
|---|---|
| AB | M |
| CD | N |
| EF | P |
Illustrations of the Midpoint
Visual representations can further enhance our comprehension. Imagine a line segment PQ. Its midpoint, R, divides the line segment into two equal parts. We can illustrate this using a number line:
P—————R—————Q
In this illustration, the distance from P to R is the same as the distance from R to Q.
General Inquiries
What is the midpoint of a line segment?
The midpoint of a line segment is the point that divides the segment into two equal parts.
How do you find the midpoint of a line segment?
The midpoint of a line segment with endpoints (x1, y1) and (x2, y2) is given by the formula: ((x1 + x2) / 2, (y1 + y2) / 2).
What are the properties of the midpoint of a line segment?
The midpoint of a line segment divides the segment into two equal parts, and it lies on the line segment.